2강 Markov Decision Processes

RL에서 가장 기본이 되는 이론인 MDP에 대해서 공부하고 정리

Markov state

• 현재 상태의 조건에서 다음 상태가 발생할 확률과 과거의 모든 상태의 조건에서 다음 상태가 발생할 확률이 같을 때, 이 때의 S_t는 Markov property라고 한다.
• 현재 주어진 상태는 과거의 모든 history 정보를 포함하고 있기 때문에 현재의 정보가 중요하며, 과거의 정보들은 의미가 없어진다.

Markov Property

•S_t가 s 인 현재 상태일 때를 조건으로 하는 S_(s+1)이 S′ 상태가 될 확률을 P_ss′로 표현

•발생하는 경우의 수를 나열하여 매트릭스의 형태로 표현

•P₁₁은 현재 상태가 1이라고 할 때 다음의 상태도 1인 경우의 확률

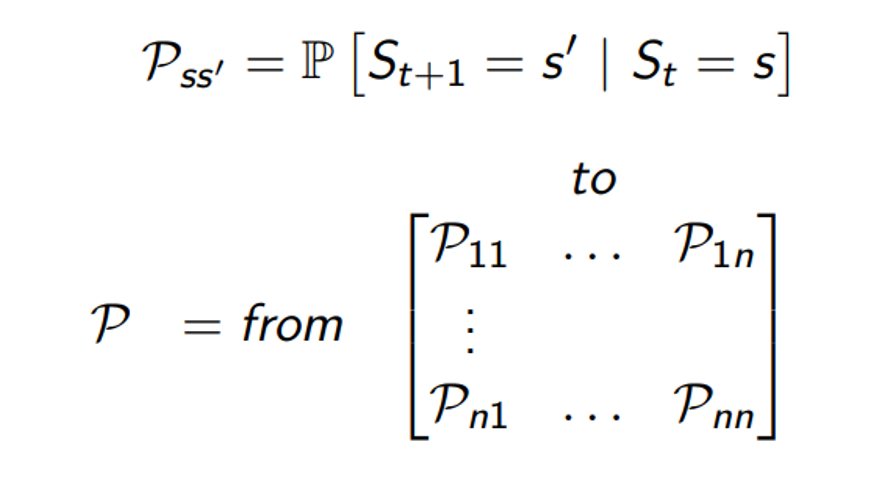
Markov Process

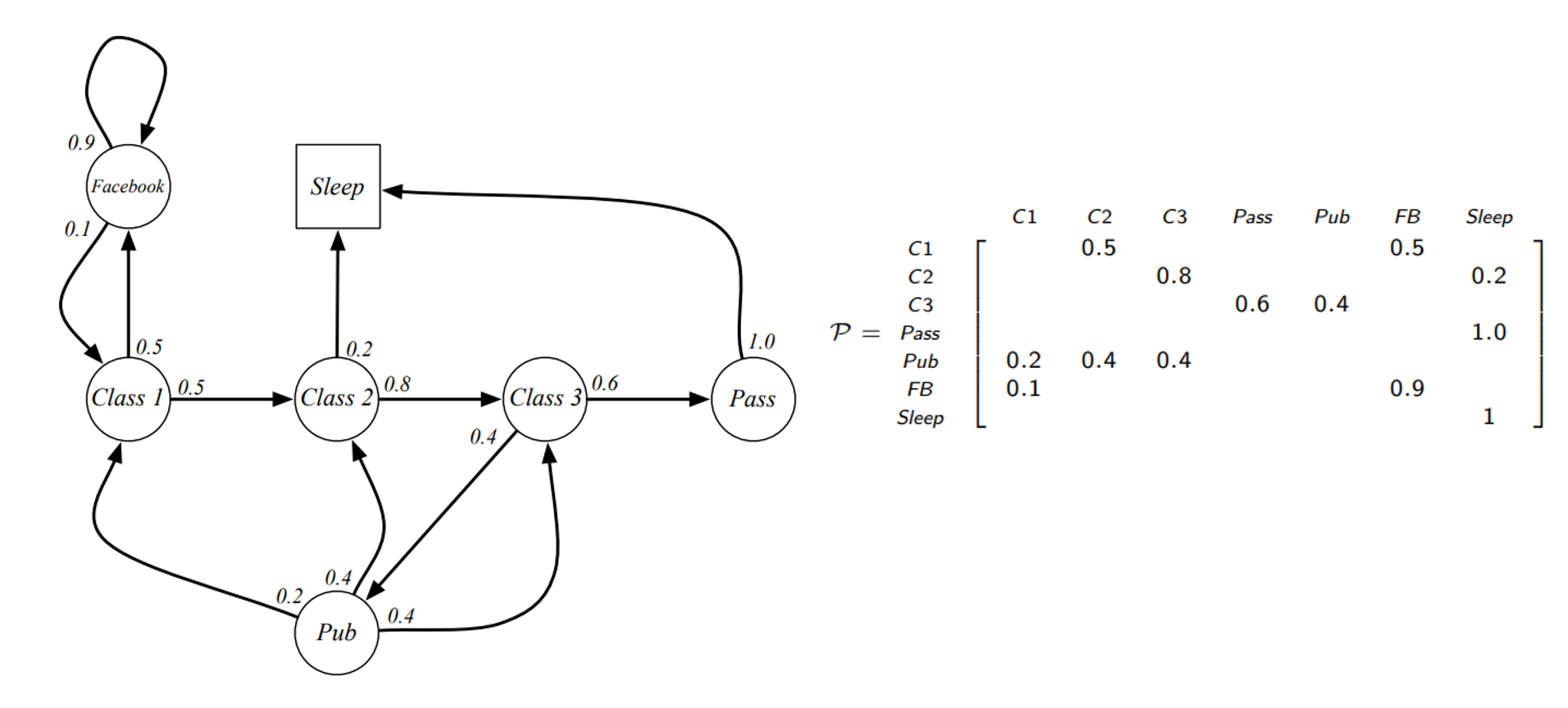
• 과거에 무엇을 했는지는 중요하지 않고 기억 하지 않음
• 현재 상태에서 하고 싶은 것 만을 랜덤하게 선택

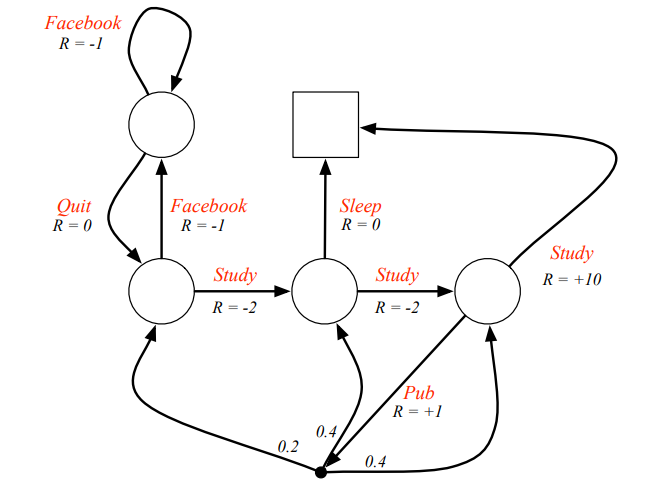
Example : Student Markov Chain

Markov Reward Process

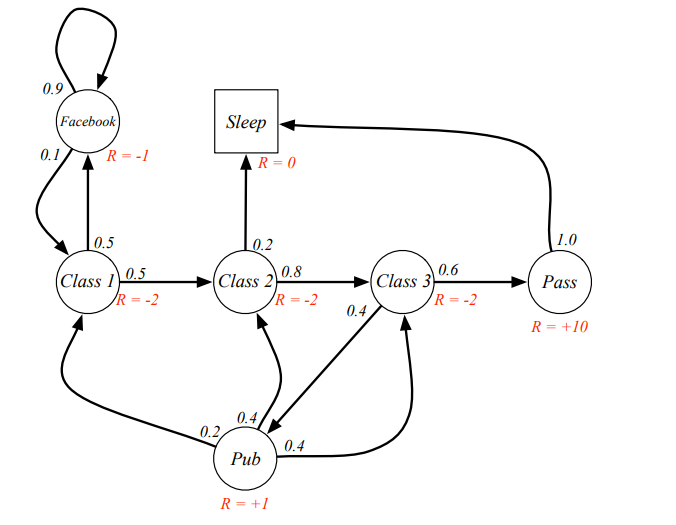
• Markov process에 values라는 개념을 추가

• 가치를 판단하기 위해 reward와 discoun factor가 있음

  

Example : Student MRP

Return / value function

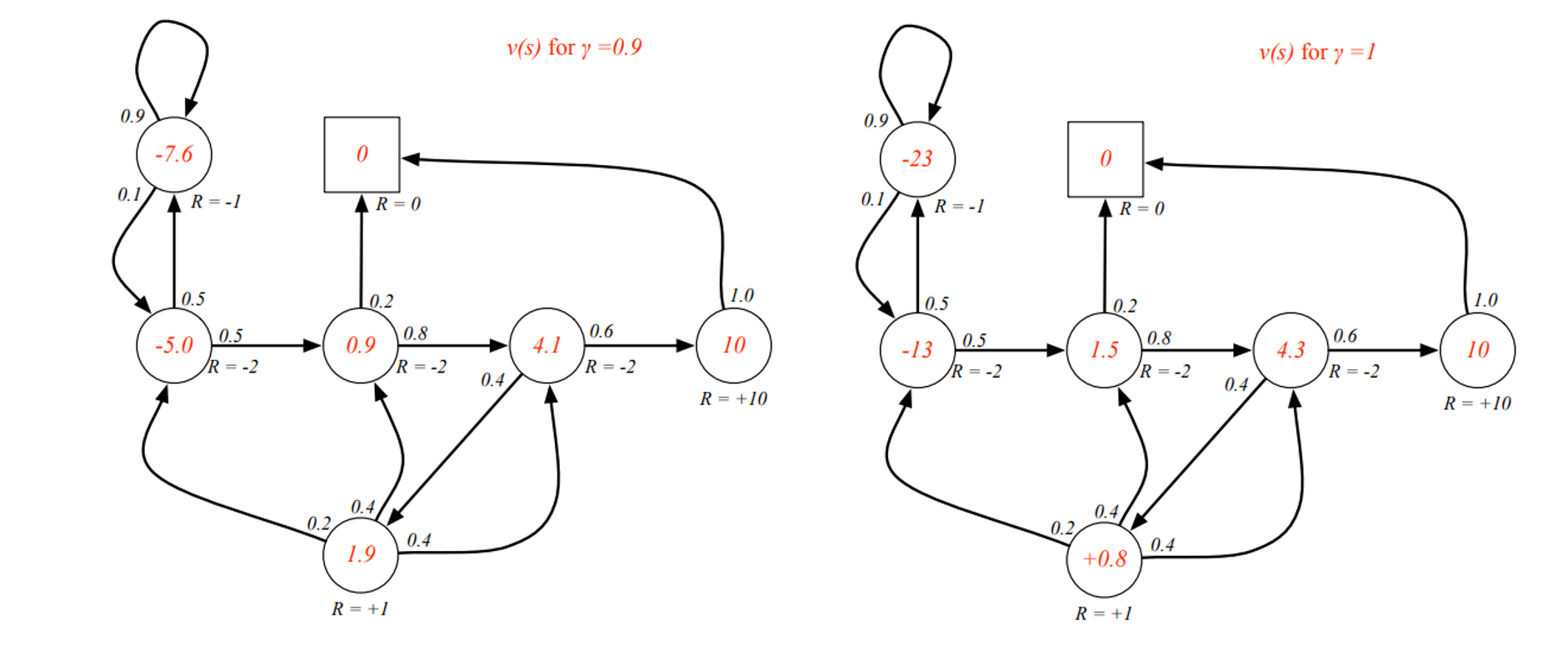
Example : Student MRP Returns

Example : State-Value Function Student MRP

Bellman Equation for MRPs

• value function을 두가지 파트로 분리 할 수 있음
• Bellman equation을 통해서 현재 시점의 value는 현재의 보상과 다음 시점의 value로 표현

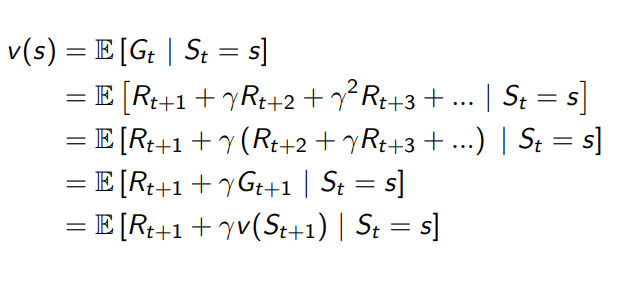
• 미래의 가치가 현재의 시점의 가치를 결정
• 밑에 부분에서의 v(s’) 두개를 합하여 할인하면 현재 시점 s의 가치를 구성하는 형태

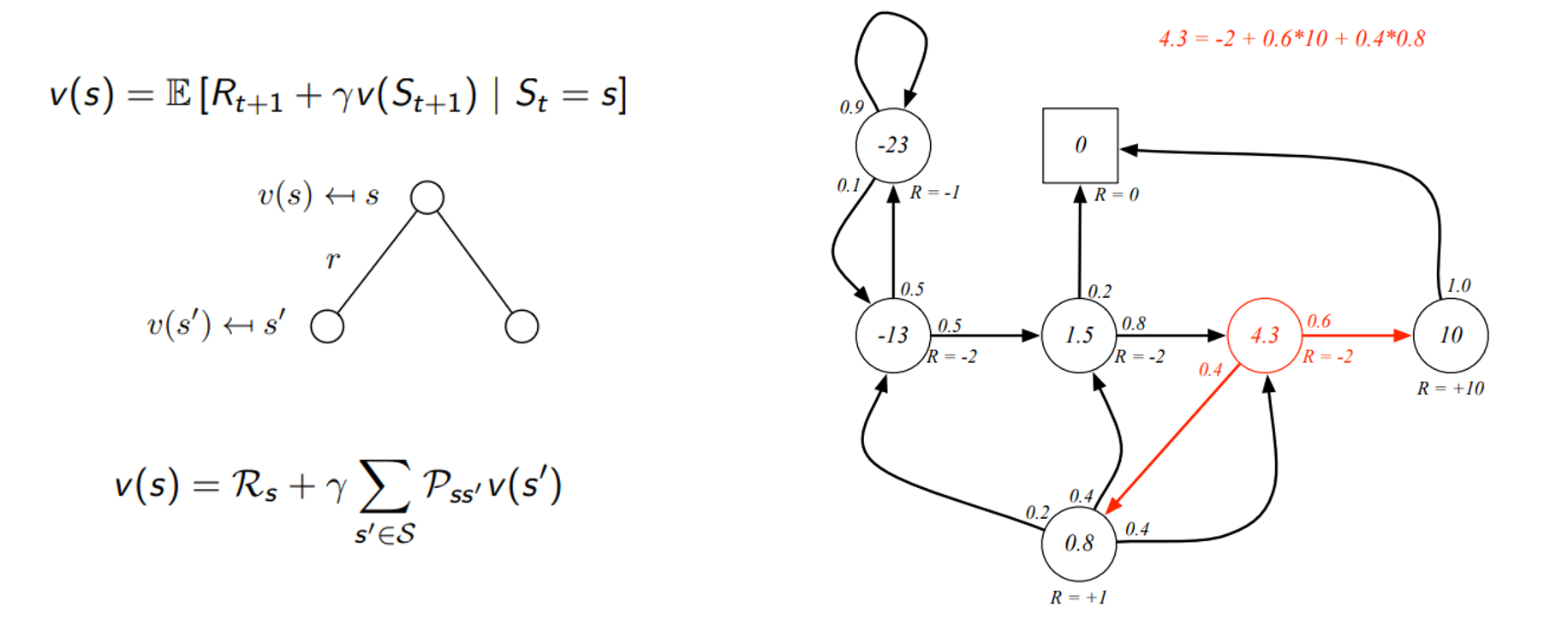
Bellman Equation in Matrix Form

• 이를 모두 표현하는 matrix형태로 표현

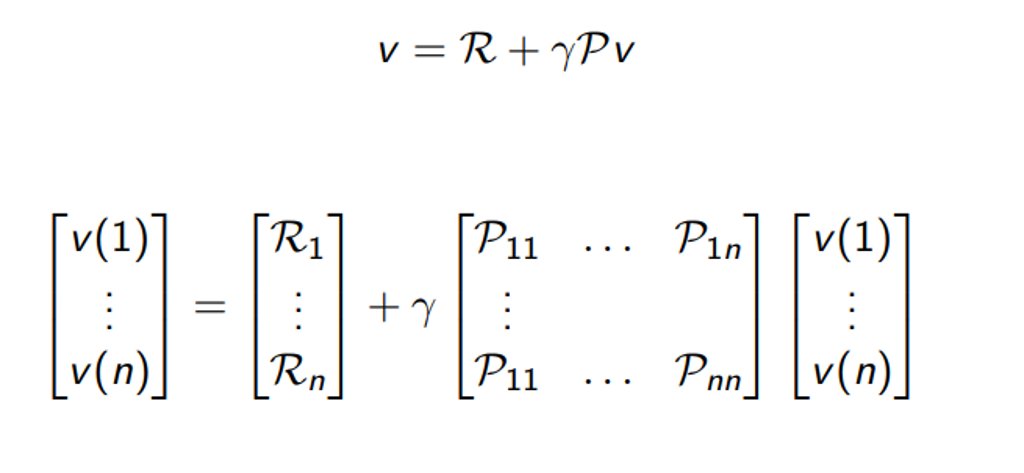
Solving the Bellman Equation

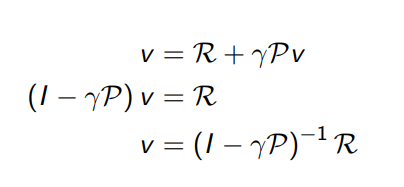
Markov Decision Process

• MRP에 의사결정에 대한 Action을 추가

Policy

• 현재 state에 대하여 어떤 action을 할 확률
• 과거의 정보는 고려하지 않고 action

• policy의 개념을 Markov process에 적용하여 표현하면 P_(s,s′)^π
• Reward에 적용하면 R_s^π

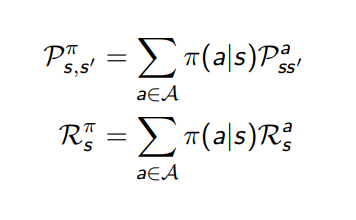
Value Function

• state s에서 policy를 따르는 v 가 되며 이것은 s에서 policy를 따르는 보상들의 모든 합
• state에 대한 value뿐만 아니라 agent가 하는 action에 대해서도 value를 측정 해야함

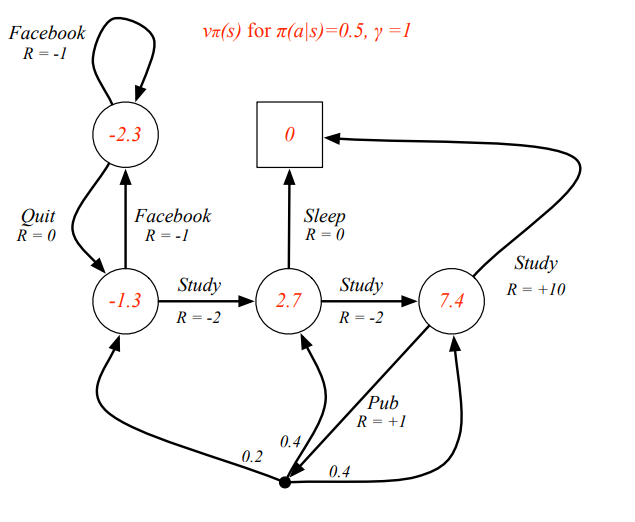
Example: State-Value Function for Student MDP

Bellman Expectation Equation

• Bellman equation을 사용해서 분리하면 다음과 같이 됨
• q도 동일하게 표현하면 s에서 어떤 a를 했을 때의 가치를 나타냄

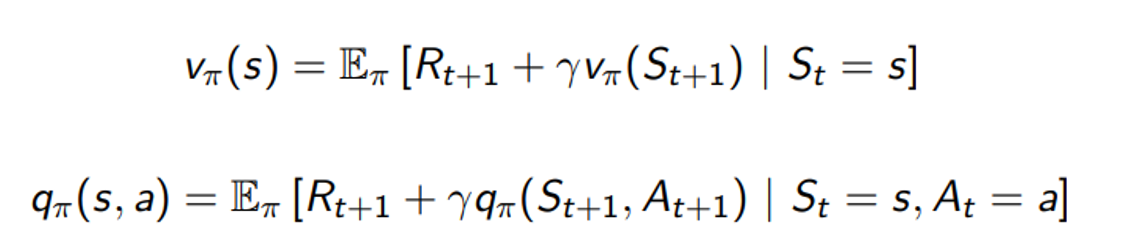
Bellman Expectation Equation for V^π

• 현재 state s에서 policy를 따르는 v는 두가지 action 중에 하나에 대한 action a을 했을 때와 나머지 action에 대한 q를 합치면 v를 구성하게 됨

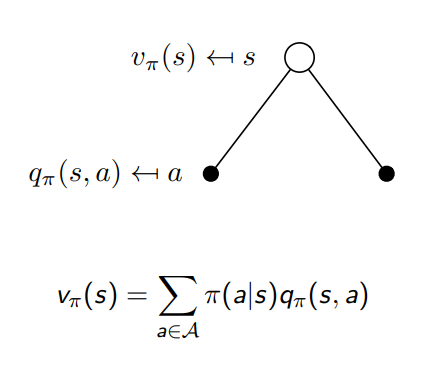
Bellman Expectation Equation for Q^π

• 또 현재 state s 에서 action a를 할 때 policy를 따르는 q 는 그로 인해서 받게 되는 reward r과 다음 state s’ 에서의 policy를 따르는 v 값에 따라 결정됨 e

  

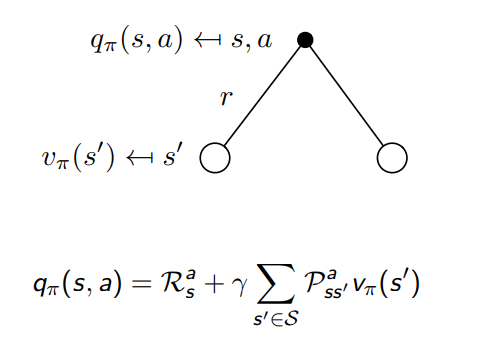
Bellman Expectation Equation for V^π, Q^π

• v 는 처음에는 q로 구성이 되었었지만 현재는 결국 다음 state의 v로만 표현이 되며, q도 마찬가지로 처음에는 v로 구성이 되었었지만 현재는 다음 state의 q로 표현이 된다는 것을 발견할 수 있음

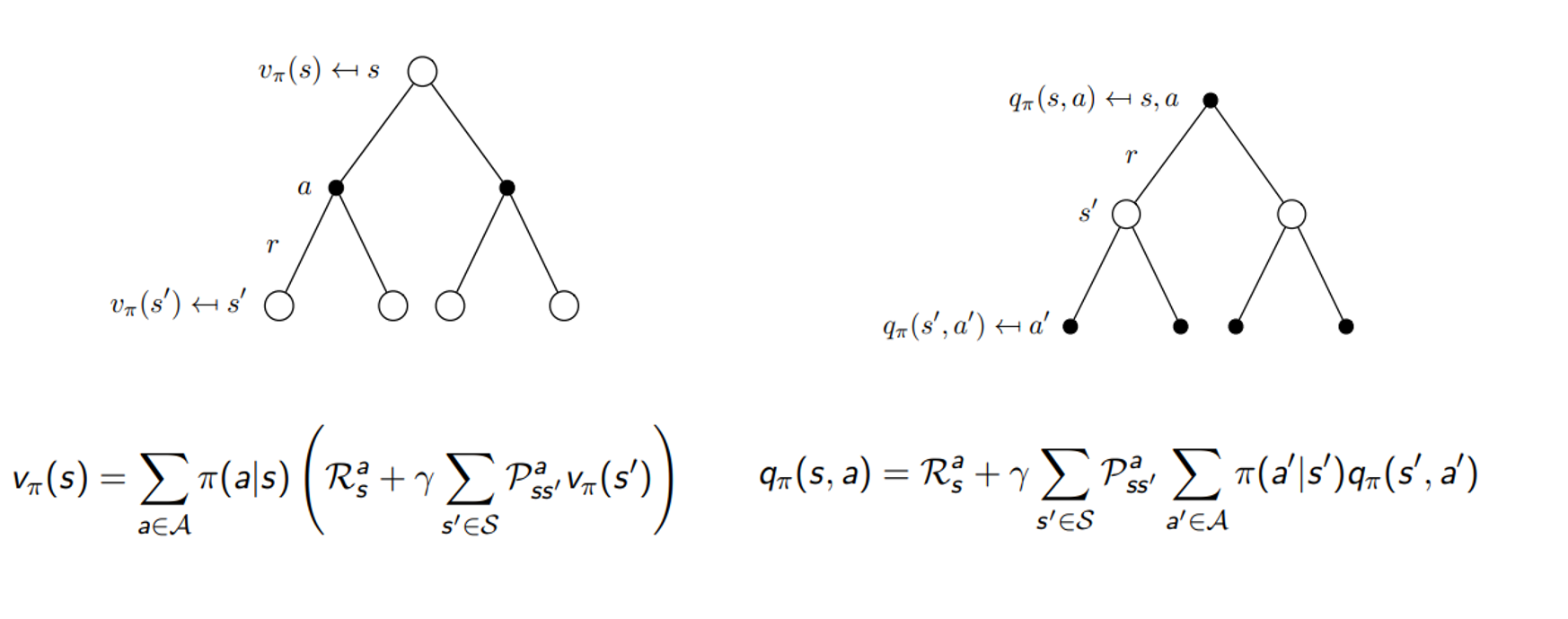
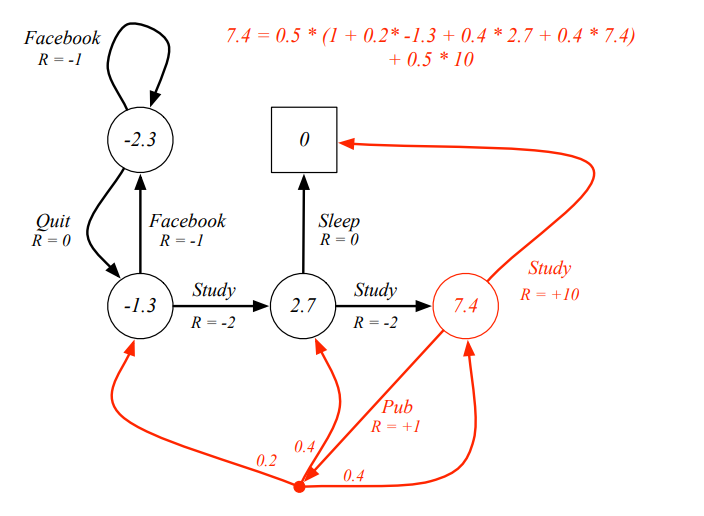
Example: Bellman Expectation Equation in Student MDP

Bellman Expectation Equation (Matrix Form)

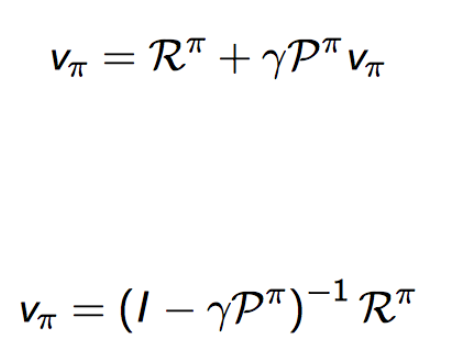
Optimal value Function

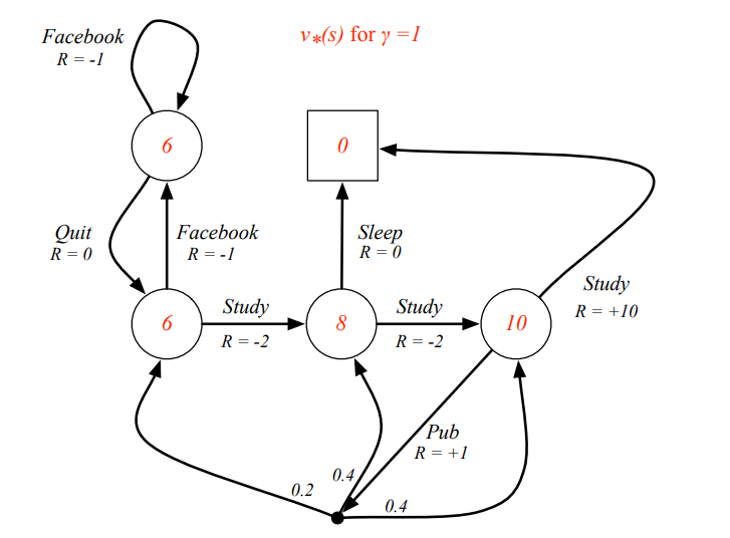
• state-value function이 갖는 값이 최대값이 되도록 함

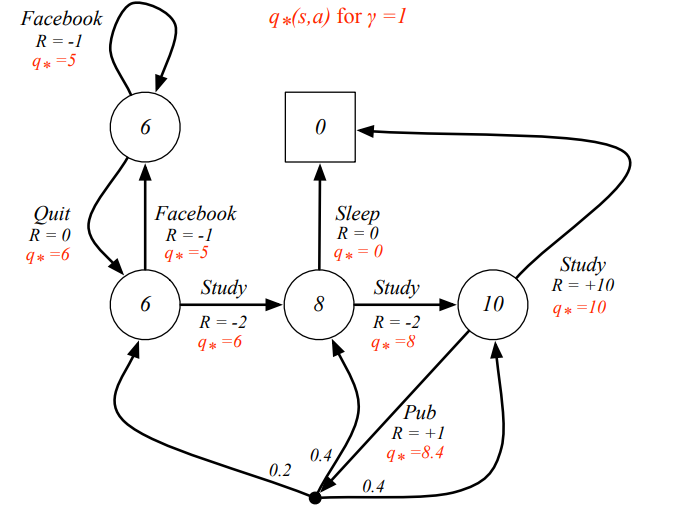
• 마찬가지로 action-value function이 갖는 값이 최대값이 되도록

  

Example: Optimal Value Function for Student MDP

Example: Optimal Action-Value Function for Student MDP

Optimal Policy

• 모든 state에 대하여, 만약 policy를 따르는 v(s)가 다른 policy’를 따르는 v(s)보다 크거나 같다면 policy가 policy’ 보다도 더 좋거나 같은 결과를 내는 정책

Finding an Optimal Policy

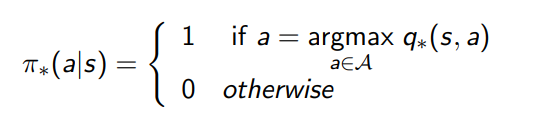
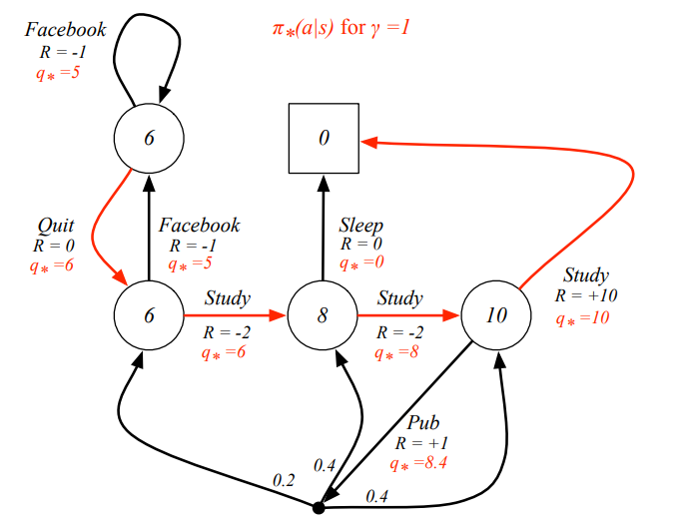
Example: Optimal Policy for Student MDP

Bellman Optimality Equation

Bellman Optimality Equation for v∗

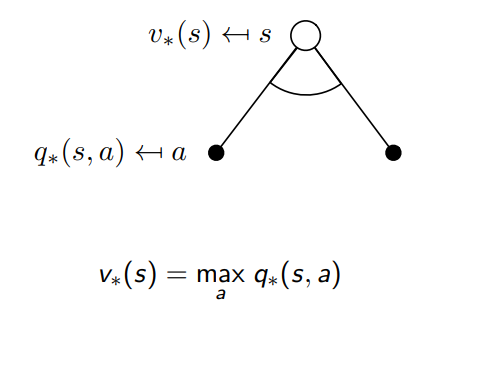
Bellman Optimality Equation for Q∗

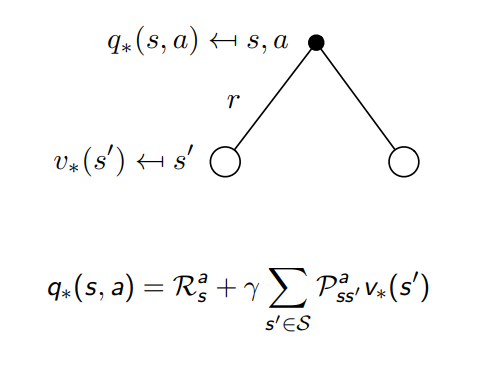
Bellman Optimality Equation for v∗

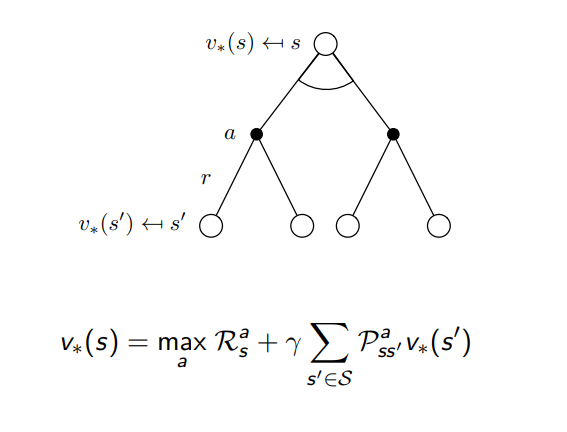
Bellman Optimality Equation for Q∗

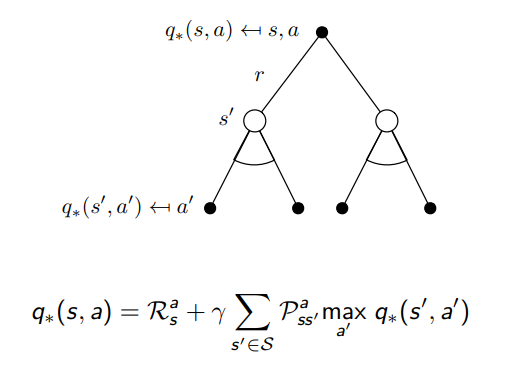
Example: Bellman Optimality Equation in Student MDP

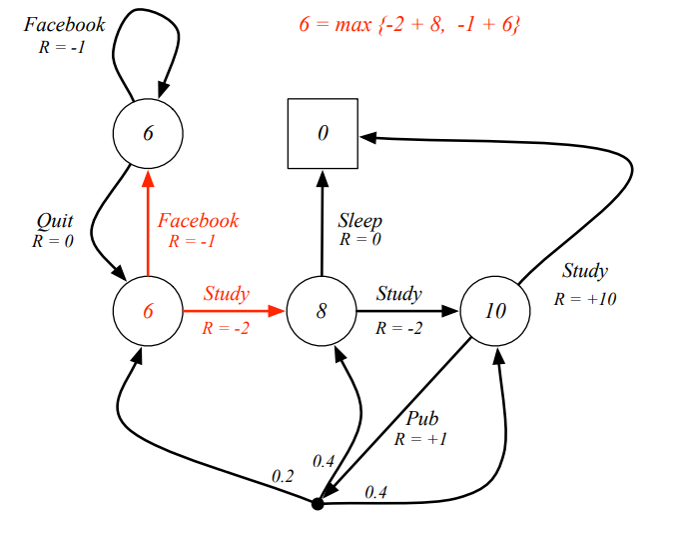
Solving the Bellman Optimality Equation