4강 Model-Free Prediction
4장은 MDP를 모르는 상황에서 환경과 직접적으로 상호작용을 하면서 경험을 통해 학습 하게 되는 방식인 MC(Monte-Carlo)와 TD(Temporal-Difference) 대해 스터디
https://mpatacchiola.github.io/blog/2017/01/15/dissecting-reinforcement-learning-2.html에서 MC, TD예시를 참고
Monte-Carlo Reinforcement Learning
- MC는 경험으로부터 직접 배우는 방법론
- Model free 방법론
- MDP의 상태 전이나 보상 함수에 관한 정보가 필요 없음
- 완전한 에피소드로부터 배움
- 에피소드가 끝나야 배울 수 있다.
- 간단한 아이디어
- 가치 = 평균 리턴
Monte-Carlo Policy Evaluation
- 목표: Policy를 이용해 얻은 에피소드들로 부터 가치 함수 𝑉π 학습
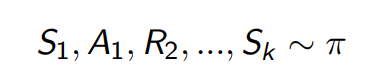
- 리턴은 누적된 보상의 합
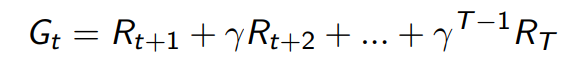
- Value function은 리턴의 기댓값 임을 기억
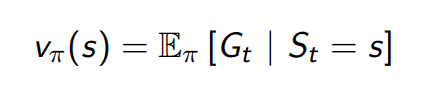
- Monte-carlo policy evaluation은 기댓값 대신에 실제 리턴의 평균을 사용
Monte-Carlo Policy Evaluation
- 상태 s의 가치를 평가하기 위해서
- 에피소드 안에서 상태 s를 방문할 때 마다
- 카운터를 증가시키고 N(s) ← N(s) + 1
- 총 리턴 값도 증가시키고 S(s) ← S(s) + G
- 가치는 그 평균으로 계산 V(s) = S(s)/N(s)
- 대수의 법칙에 의해 N(s) -> ∞ 이면 V(s) -> 𝑉π(s)
Example: Monte-Carlo Policy Evaluation(1)

Example: Monte-Carlo Policy Evaluation(2)

- the state(1, 1) is : (0.27+0.27-0.79)/3=-0.08
Incremental Mean
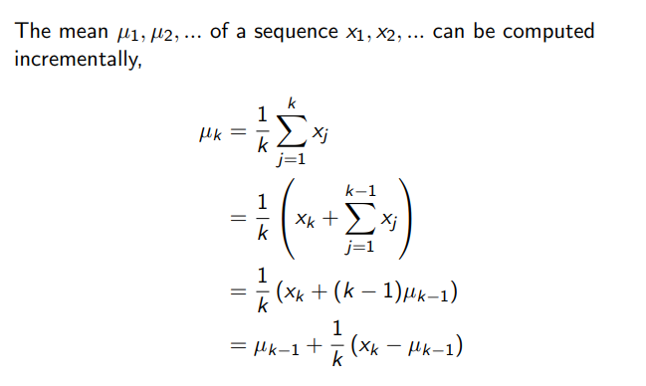
Incremental MC updates

Temporal-Difference Learning
- TD 방법론은 경험으로 부터 직접 학습
- Model Free 방법론 MDP에 대한 정보를 필요로 하지 않는다.
- 에피소드가 끝나지 않아도 학습 가능
- 추측을 추측으로 업데이트 하는 방법
MC and TD
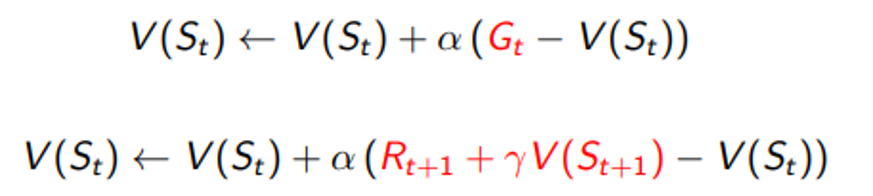
Example: Temporal-Difference
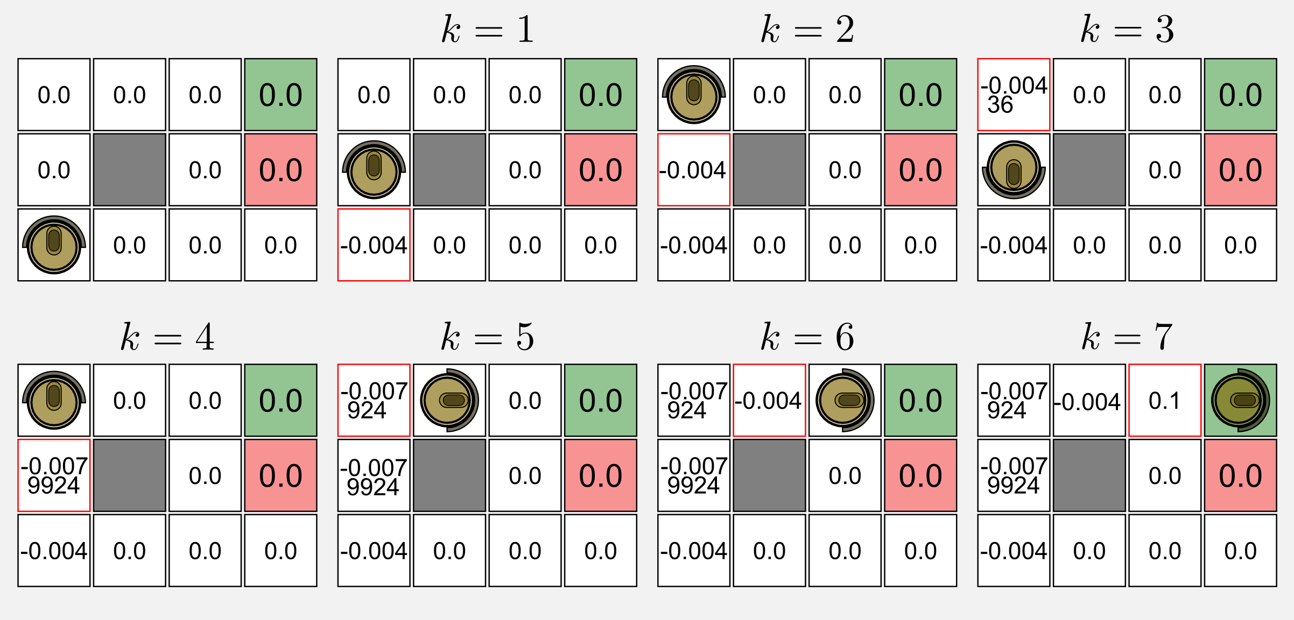
- At k=1 (1,1) : 0.0 + 0.1(-0.04 + 0.9 (0.0) – 0.0) = -0.004
- At k=3 (1,2) : 0.0 + 0.1(-0.04 + 0.9 (-0.004) – 0.0) = -0.00436
- At k=4 (1,2) : -0.004 + 0.1 (-0.04 + 0.9 (-0.00436) – (-0.004)) = -0.0079924
각 방법론의 특징
- TD는 최종 결과를 알기 전에 학습할 수 있다.
- TD는 매 스텝마다 온라인으로 학습할 수 있음.
- 반면 MC는 에피소드가 끝나서 리턴을 알게 될 때 까지 기다려야 함
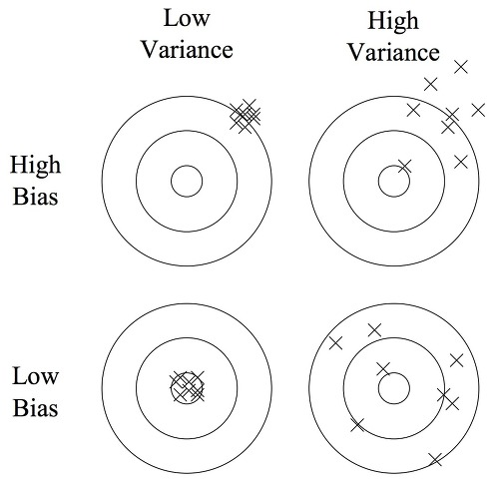
- Bias
- 리턴 Gt는 가치 함수 Vπ (St)의 unbiased estimate
- Rt+1+γVπ (St+1)도 unbiased
- 하지만 Rt+1+γV(St+1)은 biased
- Variance
- TD타겟은 리턴보다 variance가 훨씬 작음.
- 리턴은 수많은 액션, 트랜지션, 보상과 관련이 되지만 TD 타겟은 한 개의 액션, 트랜지션, 보상과 관련이 있기 때문이다.
Dynamic Programming Backup
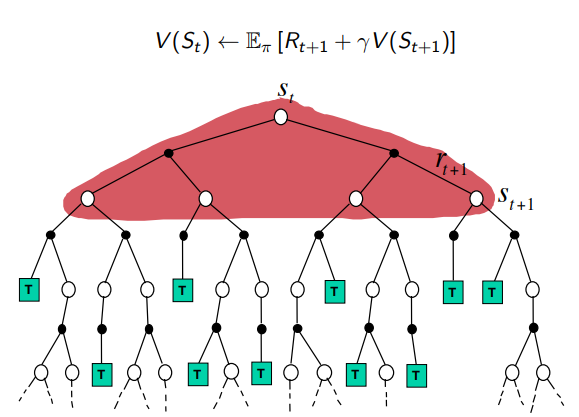
Monte-Carlo Backup
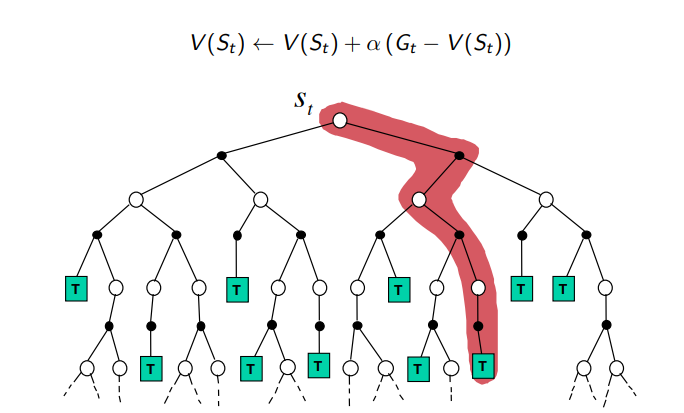
Temporal-Difference Backup
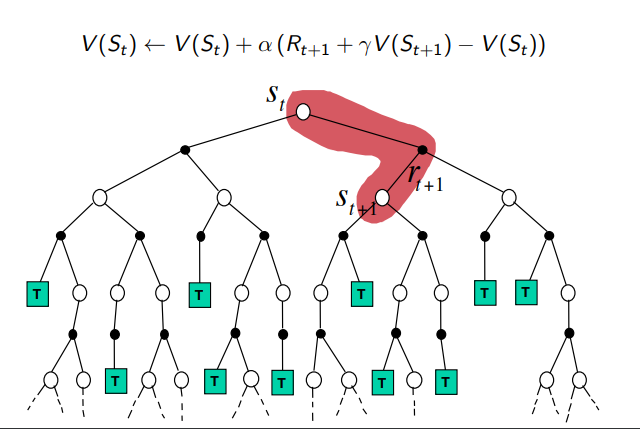
Leave a comment